A joint group in China discovered semi-Dirac semimetals as a hopeful platform to realize excitonic insulating transition.

The Coulomb interaction in the semimetals is long-ranged as the vanishing density of states at the Fermi level. A sufficiently strong long-range Coulomb could bind a gapless fermion and a gapless hole to form an excitonic pair, which generates a finite gap and turns a semimetal to an excitonic insulator

Quantum transition from semimetal to excitonic insulator in graphene attracts extensive studies, due to important potential industrial applications.

The recent theoretical and experimental studies have reached the consensus that even the strength of Coulomb interaction in the suspended intrinsic graphene is not large enough to trigger an excitonic gap.

The group led by Prof. ZHANG Changjin from High Magnetic Field Laboratory of Chinese Academy of Sciences (CHMFL) of the Chinese Academy of Sciences worked closely with the research group led by Prof. LIU Guozhu from University of Sciences of Technology of China (USTC) to conduct studies on excitonic insulator quantum transition in two dimensional semi-Dirac semimetal.

During the studies, the energy dispersion of fermion excitations is linear in one component of momenta and quadratic in the other.

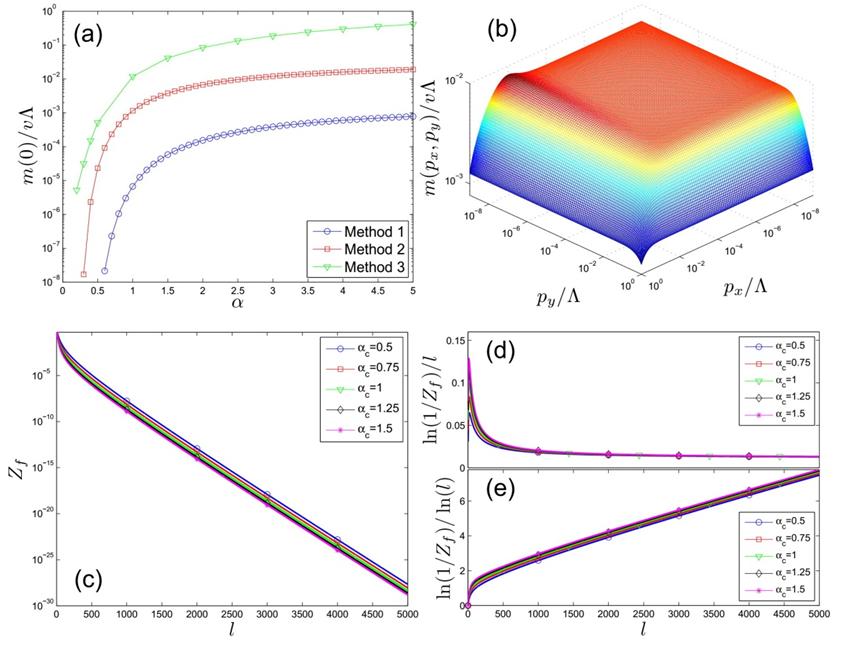
The group found that an excitonic gap can be much more easily generated in a 2D semi-Dirac semimetal than graphene, by solving the Dyson-Schwinger gap equation.

They predicted that TiO₂/VO₂ nonostructures is the most promising candidate to realize anticipated excitonic insulating state.

Meanwhile, they calculated the observable quantities analytically including density of states and specific heat in semimetal phase and insulating phase.

Lab experiments also revealed the non-Fermi liquid behaviors of semi-Dirac fermions at the semimetal-insulator quantum critical point through renormalization group (RG) method.

They reported that the wave renormalization factor approaches to zero, and the damping rate of the fermions takes power law form with the energy. It was shown that four different RG schemes give the same results.

This theoretical study provides a new and hopeful direction to experimentally realize excitonic insulating quantum transition.

The results has been published in Physical Review B entitled Excitonic pairing and insulating transition in two-dimensional semi-Dirac semimetals.

This work was supported by the National Key Research and Development Program of China, National Natural Science Foundation of China, and the Nature Science Foundation of Anhui Province.

Dynamically generated gap m and wave renormalization factor Zf.  (a) Dependence of m(0) on the Coulomb strength; (b) Dependence of the excitonic gap on the momenta；(c)-(e) Flows of wave renormalization factor Zf with the running scale l.